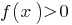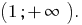2021 - 2022 навчальний рік
Тема:Показникова функція та ії властивості.
Перегляньте відео. Виконуйте завдання разом з викладачем
Відео
Откройте підручник на сторінці 7, прочитайте уважно §1
Математиshkola.in.ua › 1123-matematyka-11-klas-bevz-2019
Відповідаємо на запитання "Перевірте себе". Виконуємо завдання №№1 -7 усно і № 8, 12, 24 пісьмово.
2020 -2021 навчальний рік
Відео


f(x)=(2x2-3x+1)cosx, х=04. Периметр ромба равен 17 см. Найдите сторону ромба5. Найдите значение выражения 5sin900-ctg450+cos1800


"Від того настрою, з яким ви вступаєте в день, або в якусь справу, залежать ваші успіхи, а можливо, і невдачі". ( Конфуцій )
"Як приємно дізнатися, що ти чогось навчився " (Мольєр)
1. Скільки граней має 8-кутна призма?
а)8 , б)10 , в)6 .
2. Скільки ребер має 10-кутна призма?
а)30 , б)60 , в)10 .
3. Скільки вершин має 12-кутна призма?
а)24 , б)48 , в)12 .
4. Призма має 20 граней. Який многокутник лежить в основі?
а)20 – кутник , б)16 – кутник , в)18 – кутник .
5. Основою трикутної призми є рівносторонній трикутник. Одна з бічних граней є прямокутником, який перпендикулярний до основи. Чи буде ця призма прямою?
а)так , б)ні .
6. Яка з наведених геометричних фігур не може бути бічною гранню призми?
а)паралелограм, б) квадрат, в)трикутник, г)ромб.
7. Яка з наведених фігур може бути основою правильної призми?
а) рівнобічна б)квадрат, в)рівнобедрений г)ромб
трапеція , трикутник ,
8. За якої з наведених умов чотирикутна призма є правильною?
а)В основі лежить квадрат;
б)Усі бічні ребра призми перпендикулярні до її основи;
в)Усі бічні грані призми – рівні прямокутники;
г)За будь-якої умови .
Заповніть порожні клітинки.
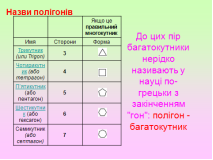
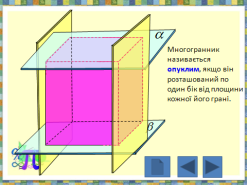
1.Многогранник, розміщений з одного боку від площини кожної його грані називають ….
2.Розрізана по кількох ребрах поверхня многогранника і розкладена на площині називається …. многогранника.
3.Тіло, поверхня якого складається зі скінченної кількості плоских многокутників, називається….
4. Площа поверхні многогранника - це….. площ усіх його граней.
5.Відрізок, який сполучає дві вершини, що не належать одній грані,-. . . многогранника





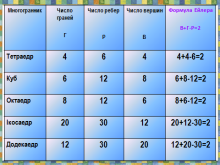
Завдання 2Підрахувати число вершин, граней і ребер у чотирикутної піраміди та виконайте для неї перевірку формули Ейлера.Починаємо знайомство з правильних просторових фігур. Назва "правильні" йде від античних часів, коли прагнули знайти гармонію, правильність, досконалість в природі і людині.
Як приклад, Пентагон (від грец.-"п'ятикутник") - назва будівлі Міністерства оборони США, що має форму правильного п'ятикутника знаходиться в штаті Вірджинія недалеко від Вашингтона.
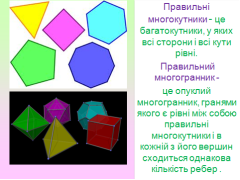
Всі правильні багатогранники були відомі ще у Стародавній Греції, їм присвячена заключна, 13-а книга знаменитих "Начал" Евкліда. Ці багатогранники часто називають також Платоновимі тілами - в ідеалістичної картині світу, даної великим давньогрецьким мислителем Платоном, чотири з них уособливали 4 стихії: тетраедр - вогонь, куб - землю, ікосаедр - воду, октаедр - повітря, додекаедр ссимволізував світобудову - його по-латині стали називати guinta essetia ( квінта есенція), що означає все найголовніше, основне, істинну сутність чого-небудь.Крім правильних многогранників, є напівправильні многогранники. Їх вперше відкрив і описав Архімед - це тіла Архімеда. Вони відрізняються від Платонових тіл тим,що їх грані- правильні багатокутники декількох типів.


Завдання 3.
Вкажіть Платонові тіла та тіла Архімеда.
Контрольна робота з теми "Логарифмічна функція. Логарифмічні рівняння та нерівності". (здати до25.12.2021. Як вирішувати дивіться уроки 35 і 36)
ЧАСТИНА 1 (3 бали )
Завдання 1 – 3 містять по 4 варіанти відповідей, з яких тільки ОДНА відповідь є ПРАВИЛЬНОЮ. Виберіть правильну, на вашу думку, відвовідь.
1. Значення виразу log 3 27 + lg 10000 дорівнює:
А) 0,0027; Б) 7; В) 12; Г) 270000.
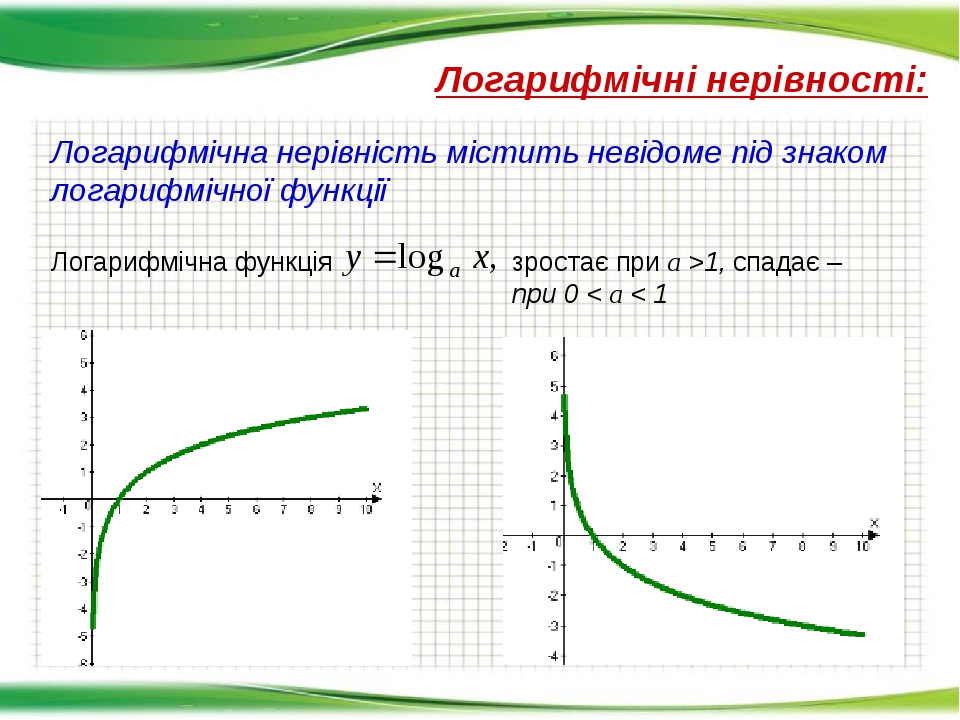
2. Областю визначення функції y = log 7 ( 2x – 1 ) є:
А) ( 2; + ∞ ); Б) ( – ∞; 2 ); В) ( 0,5; + ∞ ); Г) ( – ∞; 0,5 ).
3. Якщо log 4 m > log 4 n, то виконується умова
А) m > n; Б) m< n; В) m = n; Г) m ³ n.
ЧАСТИНА 2 ( 6 балів )
У завданнях 4 – 5 наведіть розв'язання.
4. Розв’яжіть рівняння: а) log 6 ( х-2 ) = 2;
б) log₅ (5х + 3) = log₅(7x + 5).
5. Розв’яжіть нерівність а) log 8 ( 3x + 6 ) ≥ log 8 ( 2 – x );
б) log 0,25 (x -14) > log 0,25 ( 5x + 2).
ЧАСТИНА 3 ( 3 бали )
Розв’язання завдання 6 повинне містити повне пояснення, записане у вигляді послідовних логічних дій, із посиланням на математичні факти, з яких випливає те чи інше твердження.
6. Розв’яжіть рівняння:
log22 (x - 1) - log 2 (x – 1) - 6 = 0.
Бажаю успіху!


з 31.12.2020 року розпочалися зимові канікули, які закінчуються 13.01.2020 року включно.
 |
Дорогі учні! Вітаю всіх з початком зимових канікул .


Вирішимо разом логарифмічні рівняння.

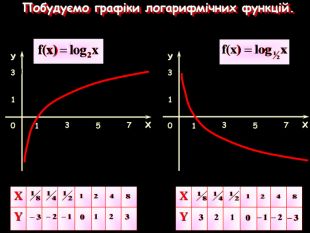
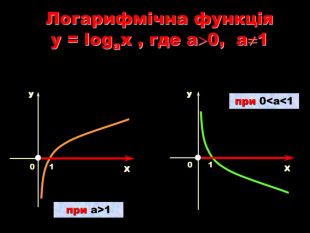
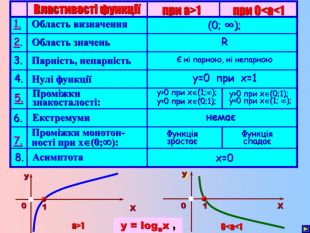

Тематична контрольна робота з теми
«Показникова функція. Показникові рівняння і нерівності»
І варіант
- Яка з наведених функцій є показниковою:
А) y=x3; Б) y=1x; В) y=(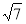 )x; Г) y=5x+3.
)x; Г) y=5x+3. - Яка з наведених показникових функцій є спадною:
А) f(x)=5x; Б) f(x)=0,2x; В) f(x)=x; Г) f(x)=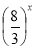 .
. - Якщо 4m > 4n, то виконується умова
А) m > n; Б) m< n; В) m = n; Г) m n. - Розв’яжіть рівняння:
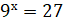
А) х=3; Б) х=-3; В) х=1,5; Г) х=-1,5.
- Розв’яжіть нерівність:
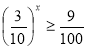 .
.
А) х≥2; Б) х≥-2; В) х≤2; Г) х≤-2.
- Розв’яжіть рівняння: 5х+3 = 625.
- Розв’яжіть нерівність:
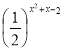 ≥ 4х-1.
≥ 4х-1.
- Розв’яжіть рівняння:
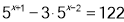
- Розв’яжіть нерівність:
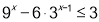
ІІ варіант
- Яка з наведених функцій є показниковою:
А) y=1x; Б) y= –x+9; В) y=x6; Г) y=(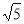 )x.
)x. - Яка з наведених показникових функцій є зростаючою:
А) f(x)=0,5x; Б) f(x)=7x; В) f(x)=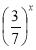 ; Г) f(x)=
; Г) f(x)= 
- Якщо 4m < 4n, то виконується умова
А) m > n; Б) m< n; В) m = n; Г) m n. - Розв’яжіть рівняння:
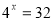 ;
;
А) х=5; Б) х=-5; В) х=2,5; Г) х=-2,5.
- Розв’яжіть нерівність:

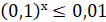 .
.
А) х ≥ 2; Б) х ≥ -2; В) х ≤ 2; Г) х ≤ -2.
- Розв’яжіть рівняння 2х-5 = 64.
- Розв’яжіть нерівність:
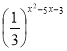 ≤ 9х-3.
≤ 9х-3.
- Розв’яжіть рівняння:
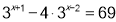
- Розв’яжіть нерівність:
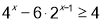

"Розум полягає не лише у знанні, але й у вмінні застосовувати ці знання"
Приклад 1. Розв'язати рівняння:
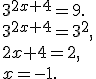
Відповідь. -1.
Приклад 2. Розв'язати рівняння: 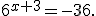
Дане рівняння коренів немає, оскільки ліва частина 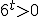 для всіх
для всіх 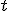 , а права -36<0.
, а права -36<0.
Відповідь. коренів немає.
Якщо в лівій і правій частинах показникового рівняння стоять тільки добутки, частки, корені або степені, то доцільно за допомогою основних формул спробувати записати обидві частини рівняння як степені з однією основою.
Приклад 3. Розв'язати рівняння:
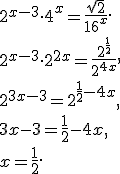
Відповідь. 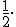
Якщо в одній частині показникового рівняння стоїть число, а в іншій всі члени містять вираз виду 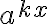 (показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь а.
(показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь а.
Приклад 4. Розв'язати рівняння:
=23,%20\\%205^{x-2}\cdot%2023=23,%20\\%205^{x-2}=1,%20\\%205^{x-2}=5^0,%20\\%20x-2=0,%20\\%20x=2.)
Відповідь. 2.
Приклад 5. Розв'язати рівняння:
^{x-0,5}}{\sqrt{5}}=5%20\cdot%20(0,04)^{x-2}.%20\\%20\frac{(5^{-1})^{x-0,5}}{5^{\frac{1}{2}}}=5%20\cdot%20(5^{-2})^{x-2};%20\\%20\frac{5^{-x+0,5}}{5^{\frac{1}{2}}}%20=5^1%20\cdot%205^{-2x+4};%20\\%205^{-x+0,5-\frac{1}{2}}=5^{1+(-2x+4)};%20\\%205^{-x}=5^{5-2x};%20\\%20-x=5-2x;%20\\x=5.)
Відповідь. 5.
У лівій і правій частинах рівняння стоять тільки добутки, частки, корені або степені. У цьому випадку для зведення рівняння до виду }=a^{g(x)}) спробуємо використати основні формули дій над степенями, щоб записати обидві частини рівняння як степені з однією основою. Слід звернути увагу на те, що
спробуємо використати основні формули дій над степенями, щоб записати обидві частини рівняння як степені з однією основою. Слід звернути увагу на те, що
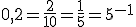 , а
, а 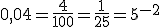
Приклад 6. Розв'язати рівняння:
^{2x-3}.%20\\%20(2%20\cdot%203)^x=(%206^{-1}%20)^{2x-3};%20\\%206^x=6^{-2x+3};%20\\%20x=-2x+3;%20\\%20x=1.)
Відповідь. -1.
Приклад 2. Розв'язати рівняння:
Дане рівняння коренів немає, оскільки ліва частина для всіх
, а права -36<0.
Відповідь. коренів немає.
Якщо в лівій і правій частинах показникового рівняння стоять тільки добутки, частки, корені або степені, то доцільно за допомогою основних формул спробувати записати обидві частини рівняння як степені з однією основою.
Приклад 3. Розв'язати рівняння:
Відповідь.
Якщо в одній частині показникового рівняння стоїть число, а в іншій всі члени містять вираз виду (показники степенів відрізняються тільки вільними членами), то зручно в цій частині рівняння винести за дужки найменший степінь а.
Приклад 4. Розв'язати рівняння:
Відповідь. 2.
Приклад 5. Розв'язати рівняння:
Відповідь. 5.
У лівій і правій частинах рівняння стоять тільки добутки, частки, корені або степені. У цьому випадку для зведення рівняння до виду спробуємо використати основні формули дій над степенями, щоб записати обидві частини рівняння як степені з однією основою. Слід звернути увагу на те, що
, а
Приклад 6. Розв'язати рівняння:
Для перетворення рівняння згадаємо, що всі формули можна використовувати як зліва направо, так і справа наліво, наприклад, для лівої частини цього рівняння скористаємося тим, що ^x=6^x.)
Відповідь. 1.
Приклад 7. Розв'язати рівняння:
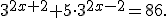
Задане рівняння рівносильне рівнянням:
=86;%20\\%203^{2x-2}%20\cdot%2086=86;%20\\%203^{2x-2}=1;%20\\%203^{2x-2}=3^0;%20\\%202x-2=0;%20\\%20x=1.)
Відповідь. 1.
У лівій частині рівняння всі члени містять вирази виду 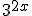 (показники степенів відрізняються тільки вільними членами). У цьому випадку зручно винести за дужки в лівій частині рівняння найменший степінь числа 3, тобто
(показники степенів відрізняються тільки вільними членами). У цьому випадку зручно винести за дужки в лівій частині рівняння найменший степінь числа 3, тобто 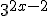 .
.
Для перетворення рівняння згадаємо, що всі формули можна використовувати як зліва направо, так і справа наліво, наприклад, для лівої частини цього рівняння скористаємося тим, що
Відповідь. 1.
Приклад 7. Розв'язати рівняння:
Задане рівняння рівносильне рівнянням:
Відповідь. 1.
У лівій частині рівняння всі члени містять вирази виду (показники степенів відрізняються тільки вільними членами). У цьому випадку зручно винести за дужки в лівій частині рівняння найменший степінь числа 3, тобто
.
Рівносильні перетворення найпростіших нерівностей
 При а > 1
При а > 1
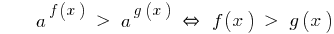
Знак нерівності зберігається.
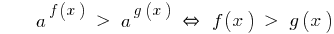
Приклад 1
Розвяжіть нерівність: 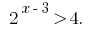
Розвязання:
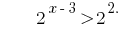
Функція 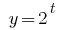 є зростаючою, отже прирівнюємо показники,
є зростаючою, отже прирівнюємо показники,
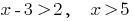
Відповідь: 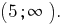
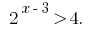
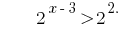
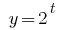 є зростаючою, отже прирівнюємо показники,
є зростаючою, отже прирівнюємо показники,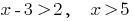
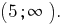
 При 0 < а < 1
При 0 < а < 1
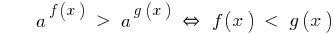
Знак нерівності змінюється на протилежний.
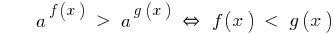
Приклад 2
Розвяжіть нерівність: 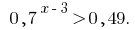
Розвязання:
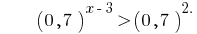
Функція y=0,7^t~ є спадною, отже прирівнюємо показники,
x - 3 < 2, x < 5.
Відповідь: 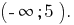
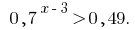
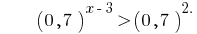
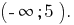
Розвязування більш складніших показникових нерівностей
Приклад 3
Розвяжіть нерівність: 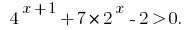
Розвязання:
Заміна 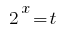 дає нерівність
дає нерівність 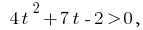
розвязки якої 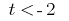 або
або 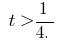
Отже 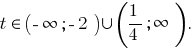
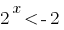 (розвязків немає) або
(розвязків немає) або 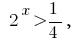 звідки
звідки 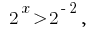 тобто
тобто 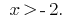
Відповідь: 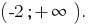
За допомогою загального методу інтервалів
Застосовуємо загальний метод інтервалів,
- Знайти ОДЗ
- Знайти нулі функції

- Позначити нулі функції на ОДЗ і знайти знак
 у кожному з проміжків, на які розбивається ОДЗ.
у кожному з проміжків, на які розбивається ОДЗ. - Записати відповідь, ураховуючи знак нерівності.
Приклад 4
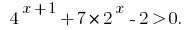

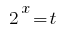 дає нерівність
дає нерівність 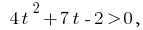
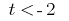 або
або 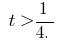
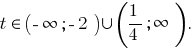
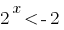 (розвязків немає) або
(розвязків немає) або 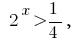 звідки
звідки 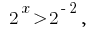 тобто
тобто 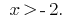
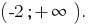

 у кожному з проміжків, на які розбивається ОДЗ.
у кожному з проміжків, на які розбивається ОДЗ.Розвяжіть нерівність: 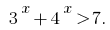
Розвязання:
Розвяжемо нерівність методом інтервалів. Задана нерівність рівносильна нерівності 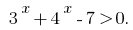
Позначимо 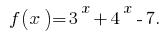
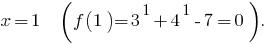
- ОДЗ:
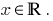
- Нулі функції:
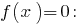
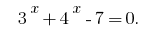
- Оскільки функція
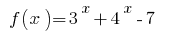 є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення:
є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення: - Позначимо нуль функції на ОДЗ, знаходимо знак
 у кожному з проміжків, на які розбвається ОДЗ, і записуємо розвязки нерівності
у кожному з проміжків, на які розбвається ОДЗ, і записуємо розвязки нерівності 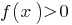
Відповідь: 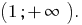
30.11.2020.
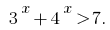

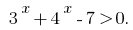
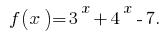
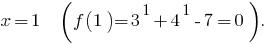
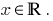
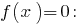
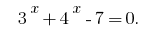
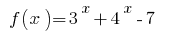 є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення:
є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення: у кожному з проміжків, на які розбвається ОДЗ, і записуємо розвязки нерівності
у кожному з проміжків, на які розбвається ОДЗ, і записуємо розвязки нерівності