2021 -2022 навчальний рік.
25.10.2021.(2уроки)
А) 486 см3; Б) 693 см3; В) 321 см3; Г) 231 см3.
Дано:
SAВСD - піраміда, АВСD - прямокутник, АВ = 7 см., АD = 11 см , SO = 9см.
Знайти: VSABCD
Розв'язування: Об'єм піраміди знаходиться за формулою : V = 1/3・Socн ・H, д де Sосн - площа основи, тобто прямокутника АВСD , H - висота SO.

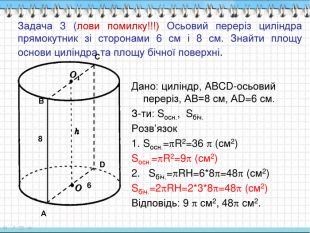
А) 18π см2 ; Б) 36π см2 ; В) 144π см2 ; Г) 12π см2 .
А) 40π см2 ; Б) 60π см2 ; В) 80π см2 ; Г) 100π см2 .
Розв'язання:
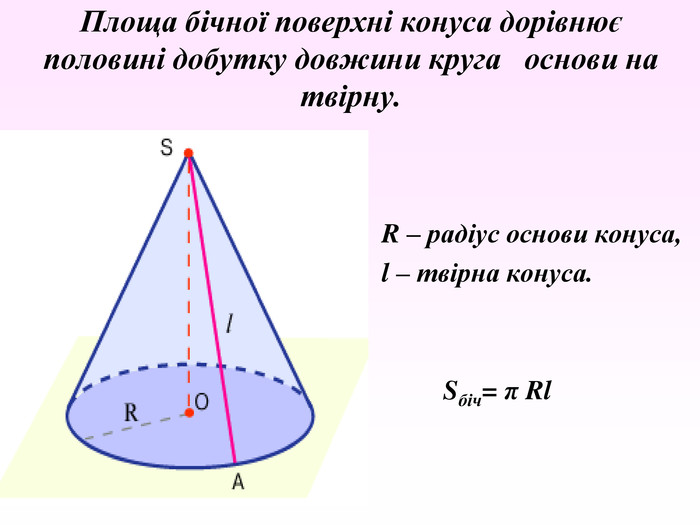
За умовою завдання H = SO = 8 cм, діаметр D = 2R = 2AO =12 cм, звідси AO = 6 cм,
21.10.2021.
Відео
11 запитань. Самостійна робота.Запитання 1Куля це -
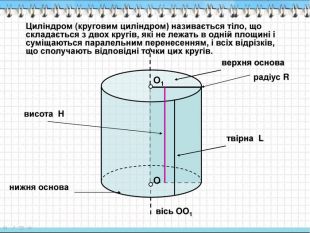
Запитання 2Сфера це -
Запитання 3Площину, що має зі сферою одну спільну точку, називають -
Запитання 4Радіус кулі дорівнює √3 см. Яка точка належить кулі, якщо вона віддалена від центра кулі:
Запитання 5Сфера перетинається площиною, відстань від якої до центра сфери дорівнює 6 см. Довжина лінії перетину сфери з площиною дорівнює 16π см. Знайдіть радіус сфери.
Запитання 6На сфері із центром О позначили точки А і В такі, що АВ=18 см. Знайдіть радіус сфери, якщо відстань від точки О до прямої АВ дорівнює 12 см.
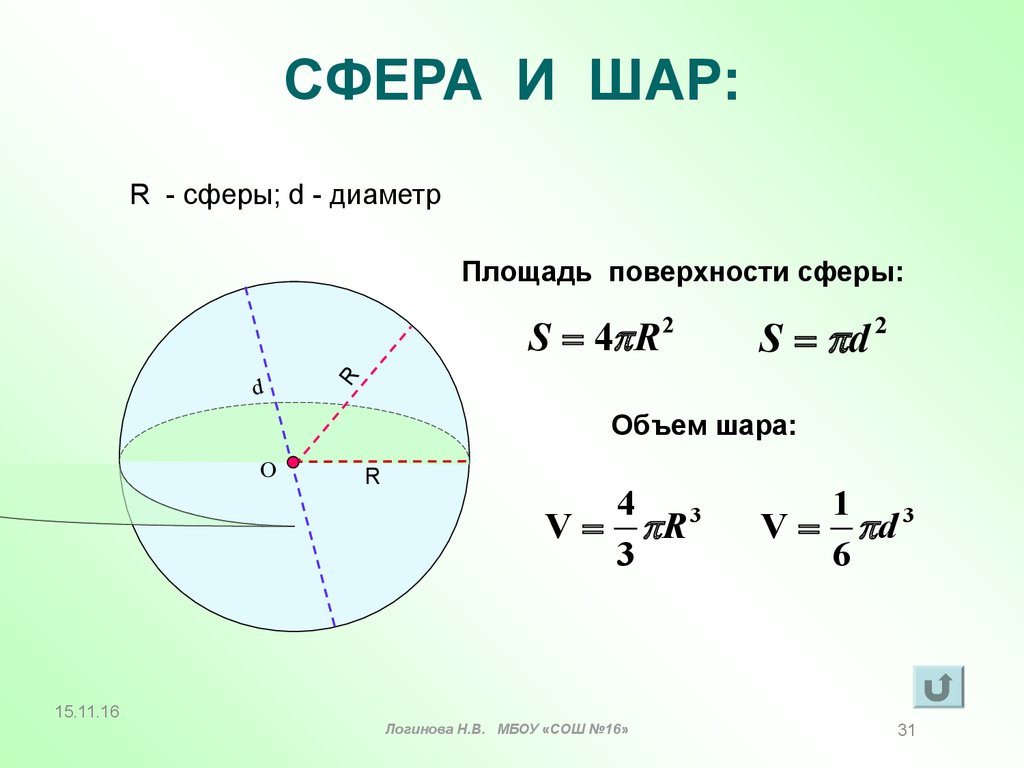
Запитання 7Діаметр кулі дорівнює 6 см. Знайти площу поверхні кулі.
Запитання 8Формула площі поверхні сфери має вигляд:
Запитання 9Радіус сфери дорівнює 7 см. Знайти площу поверхні сфери.
Запитання 10Площа поверхні сфери дорівнює 324π см2 . Знайти діаметр сфери.
Запитання 11Кулю радіуса 41 см перетнули площиною. Площа перерізу дорівнює 1600π см2. На якій відстані від центра кулі проведено площину?
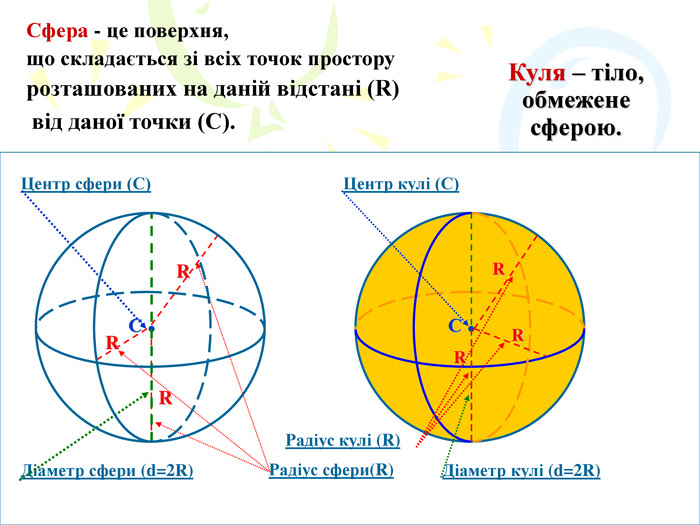
Куля це -
Сфера це -
Площину, що має зі сферою одну спільну точку, називають -
Радіус кулі дорівнює √3 см. Яка точка належить кулі, якщо вона віддалена від центра кулі:
Сфера перетинається площиною, відстань від якої до центра сфери дорівнює 6 см. Довжина лінії перетину сфери з площиною дорівнює 16π см. Знайдіть радіус сфери.
На сфері із центром О позначили точки А і В такі, що АВ=18 см. Знайдіть радіус сфери, якщо відстань від точки О до прямої АВ дорівнює 12 см.
Діаметр кулі дорівнює 6 см. Знайти площу поверхні кулі.
Формула площі поверхні сфери має вигляд:
Радіус сфери дорівнює 7 см. Знайти площу поверхні сфери.
Площа поверхні сфери дорівнює 324π см2 . Знайти діаметр сфери.
Кулю радіуса 41 см перетнули площиною. Площа перерізу дорівнює 1600π см2. На якій відстані від центра кулі проведено площину?












1. Радіус конуса – 3 см, твірна – 5 см.
Висота конуса дорівнює:
а)
2√3 см;
б)
2 см;
в)
6 см;
г) 4
см.
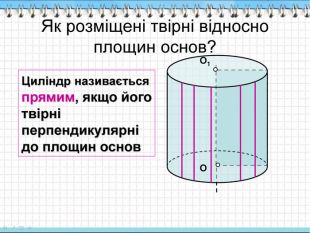
2. Конус – це тіло обертання:
а) прямокутника навколо його сторони;
б) рівнобедреного трикутника навколо
його сторони;
в) прямокутного трикутника навколо його гіпотенузи;
г) прямокутного трикутника навколо його
катета.
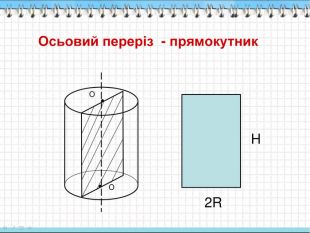
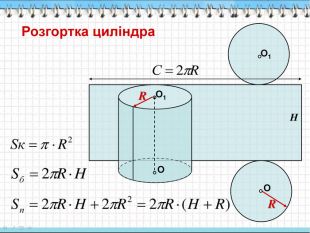
3. Формула площі повної поверхні
циліндра:
а) 2πRh + πR²;
б) 2πR(h + R);
в) πRl +πR² ;
г) 4πR².
4. Радіус сфери, площа якої дорівнює 676![]() дм2 дорівнює:
дм2 дорівнює:
а)
12 дм;
б) 13
дм;
в)
169 дм;
г)
26 дм.
5. Знайдіть площу сфери, діаметр якої
дорівнює 30 см.
6. Знайдіть площу конуса з радіусом 13 см, якщо його твірна дорівнює 28 см.
7. Радіус основи циліндра 2 м, висота – 3 м. Знайдіть діагональ та площу осьового
перерізу.
8. Знайдіть площу основи конуса, твірна
якого дорівнює 12 см, а площа бічної
поверхні - 504![]() см2.
см2.
9. Кулю радіуса 10 см перетинає площина, віддалена від її центра на 6 см. Знайдіть
площу перерізу.
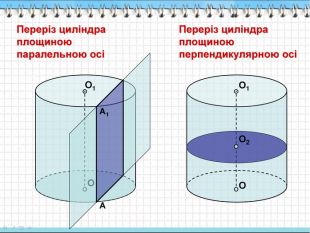
10.Висота циліндра 6 дм, радіус основи 5 дм.
Знайдіть площу перерізу, проведеного
паралельно осі циліндра на відстані 4
см від неї.
Удачи!















Задача 1 "Громовідвід"
Обчислити висоту громовідводу та площу, яку він захищає, якщо
радіус "захищеного" круга 50 м, а кут між громовідводом і
твірною конуса безпеки 60 0
Розв’язання:
h= 50м : tg 60°= 29,4м
S= 3.14 *2500 = 7850м2= 78,5а
Відповідь: 29,4м; 78,5а
Корінне населення, яке проживає на далекій Півночі, ненці, веде
напівкочовий спосіб життя і проживають вони в чумах.
Задача 2
Скільки потрібно оленячих шкур, площею 3,8 м2, для
покриття чума, якщо діаметр основи 16м, а основна жердина √20м.
Розв’язання
R = 16:2 = 8(м)
L2= √202 +
82 =84, L = 2√21м
S = 3,14*8*2√21= 230,23 (м2)
230,23: 3,8 = 60,6 ≈61(штук)
Ви вже умієте знаходити
елементи конуса,його поверхню, але чи зможете ви їх застосовувати в
практичній діяльності. Адже купа щебеню біля краю дороги чи на
будівельному майданчику також заслуговує на увагу. Дивлячись на неї, ми
можемо задати собі питання :
Яку площу займає щебінь?
Яка поверхня цієї купи щебеню?
Задача досить складна для людини, яка звикла долати труднощі
на папері або на класній дошці. Адже необхідно обчислити поверхню конуса,
висота і радіус якого недоступні для безпосереднього вимірювання.
Задача 3:
Нехай довжина основи конічної купи щебеню 12м. Довжина двох
твірних 4,6 м. Знайти площу поверхні купи щебеню.
Розв’язок:
L = 4,6/2 = 2,3 м
R = С/2ㄫ = 12 /6,28 = 1,9 м
Sбічн = π · R · L = 3,14 * 1,9*2,3 = 13,7м2
Відповідь: 13,7 м2
Задача 5
Верхня частина башні має форму конуса, радіус основи якого 11/πм,
а твірна 9м..Бічну поверхню планують покрити мозаїкою. Скільки мішків
клею потрібно купити для виконання цієї роботи, якщо витрати клею 5 кг на 1м2,
а в одному мішку 25 кг клею?
Розв’язок:
Sбічн=πRL
S = π*11/π*9= 99м2
25:5 = 5м2 ; 99: 5 = 19,8 ( мішків)
Відповідь: 20 мішків
Самост ійна робот.а.
1. Конічна куча зерна має висоту
2. Скільки потрібно
працівників для перенесення дубової балки розміром 6,5м х 30см х 4,5 дм? Кожен
працівник може підняти в середньому
80кг. Густина дуба дорівнює 800кг/м3
3. Скільки тон
розчину треба приготувати для зовнішнього оштукатурення будинку, довжина якого
37м, ширина –
4. Вугілля насипане в купу, яка має форму конуса з кутом
укосу 300. Діаметр основи кучі
= ![]() Вага вугілля = 2000кг/м3.
Вага вугілля = 2000кг/м3.




Тетраедр в архітектурі:
|
У Новому Орлеані розроблено “Будівлю місто”, висота
якої 365 метрів, вона включає в себе 20 000 квартир, загальна площа
2 040 000 м кв. Будівля використовує екологічні енергоносії
– енергію вітру, води і сонця. Крім квартир, в тетраедрі розташовані
комерційні організації, 3 готелі, культурні об’єкти, школа, лікарня. |
|
Враховуючи місце, під яке створювався проект, його
дуже важлива особливість – здатність триматися на плаву.
От що буває від
великого розуму. Хоча, голова корисна – оскільки в ній розміщена адміністрація
міської бібліотеки.
Алмаз – це дорогоцінний кристал і
є найтвердішим з речовин. У промислові алмази, завдяки їх надзвичайній твердості,
використовують для шліфування, свердління і різання, буріння твердих гірських
порід, обробки твердих металів та інших сплавів тощо.
|
Огранені ювелірні алмази
називають діамантами. За останніми дослідженнями в Україні виявлені дві
перспективні ділянки щодо знаходження алмазоносних кімберлітів, які
розташовані на Донеччині і Рівненщині. Вірус герпесу |
|
Вирішите завдання:
1) У тетраедра площа однієї
грані 4 см². Знайти площу всього тетраедра.
2)
Скільки потрібно дроту, щоб
виготовити куб, ребро якого дорівнює 20 см?![]()
3) Знайти периметр однієї
грані октаедра, якщо його ребро дорівнює 5 см?
4) Площа однієї
грані гексаедра дорівнює 144 см2. Знайдіть діагональ цього
многогранника.
Вихором надії, хуртовиною щастя нехай кружляє Вас Новий 2021 рік!
Нехай несе він радісні зміни, наповнює будні успіхом, виконує грандіозні плани, надає прекрасні можливості і перспективи, дарує Вам міцне здоров’я, невичерпний оптимізм та тверду віру . З новим роком!
"Від того настрою, з яким ви вступаєте в день, або в якусь справу, залежать ваші успіхи, а можливо, і невдачі". ( Конфуцій )
"Як приємно дізнатися, що ти чогось навчився " (Мольєр
Тестові завдання.
1. Скільки граней має 8-кутна призма?
а)8 , б)10 , в)6 .
2. Скільки ребер має 10-кутна призма?
а)30 , б)60 , в)10 .
3. Скільки вершин має 12-кутна призма?
а)24 , б)48 , в)12 .
4. Призма має 20 граней. Який многокутник лежить в основі?
а)20 – кутник , б)16 – кутник , в)18 – кутник .
5. Основою трикутної призми є рівносторонній трикутник. Одна з бічних граней є прямокутником, який перпендикулярний до основи. Чи буде ця призма прямою?
а)так , б)ні .
6. Яка з наведених геометричних фігур не може бути бічною гранню призми?
а)паралелограм, б) квадрат, в)трикутник, г)ромб.
7. Яка з наведених фігур може бути основою правильної призми?
а) рівнобічна б)квадрат, в)рівнобедрений г)ромб
трапеція , трикутник ,
8. За якої з наведених умов чотирикутна призма є правильною?
а)В основі лежить квадрат;
б)Усі бічні ребра призми перпендикулярні до її основи;
в)Усі бічні грані призми – рівні прямокутники;
г)За будь-якої умови .
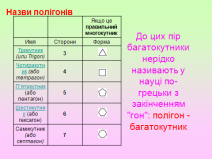
Заповніть порожні клітинки.
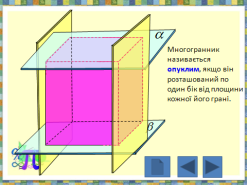
1.Многогранник, розміщений з одного боку від площини кожної його грані називають ….
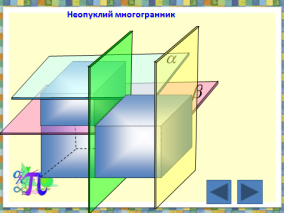
2.Розрізана по кількох ребрах поверхня многогранника і розкладена на площині називається …. многогранника.
3.Тіло, поверхня якого складається зі скінченної кількості плоских многокутників, називається….
4. Площа поверхні многогранника - це….. площ усіх його граней.
5.Відрізок, який сполучає дві вершини, що не належать одній грані,-. . . многогранника
9.12.2020. УРОК 40












7.12.2020. УРОКИ 38 і 39
Тема: Контрольна робота з теми "Логарифмічна функція. Логарифмічні рівняння та нерівності".
ЧАСТИНА
1 / 3 бали
/
Завдання 1 – 3 містять по 4 варіанти відповідей, з яких тільки ОДНА відповідь є ПРАВИЛЬНОЮ. Виберіть правильну, на вашу думку, відвовідь.
1.
Значення
виразу log 3 27 + lg 10000 дорівнює:
А) 0,0027; Б) 7; В) 12;
Г) 270000.
2.
Областю
визначення функції y
= log 7
( 2x – 1 )
є:
А) ( 2; + ∞ ); Б) ( – ∞; 2
); В) ( 0,5; + ∞ ); Г) ( – ∞; 0,5 ).
3.
Якщо log 4
m > log 4
n, то виконується умова
А) m > n; Б) m<
n; В) m = n; Г) m ³ n.
ЧАСТИНА
2 / 6 балів
/
У завданнях 4 – 6 наведіть розв'язання.
4. Розв’яжіть рівняння: а) log 6 ( х-2 ) = 216; б) log х 125 = 3.
5. Розв’яжіть нерівність а) log 8 ( 3x + 6 ) ≥ log 8 ( 2 – x )
б) log 0,25 (x -14) > log 0,25 ( 5x + 2)
6. Розв’яжіть рівняння: log 0,8 x + log 0,8 ( x – 1 ) = log 0,8 ( x + 3)
ЧАСТИНА
3 / 3 бали
/
Розв’язання завдання 7 повинне містити повне пояснення, записане у вигляді послідовних логічних дій, із посиланням на математичні факти, з яких випливає те чи інше твердження.
7.
Розв’яжіть
рівняння:
log22 (x - 1) - log 2 (x – 1) - 6 = 0.
Бажаю успіху!
Відео
1

2

3

4

5

30.11.2020. УРОК 35 і 36
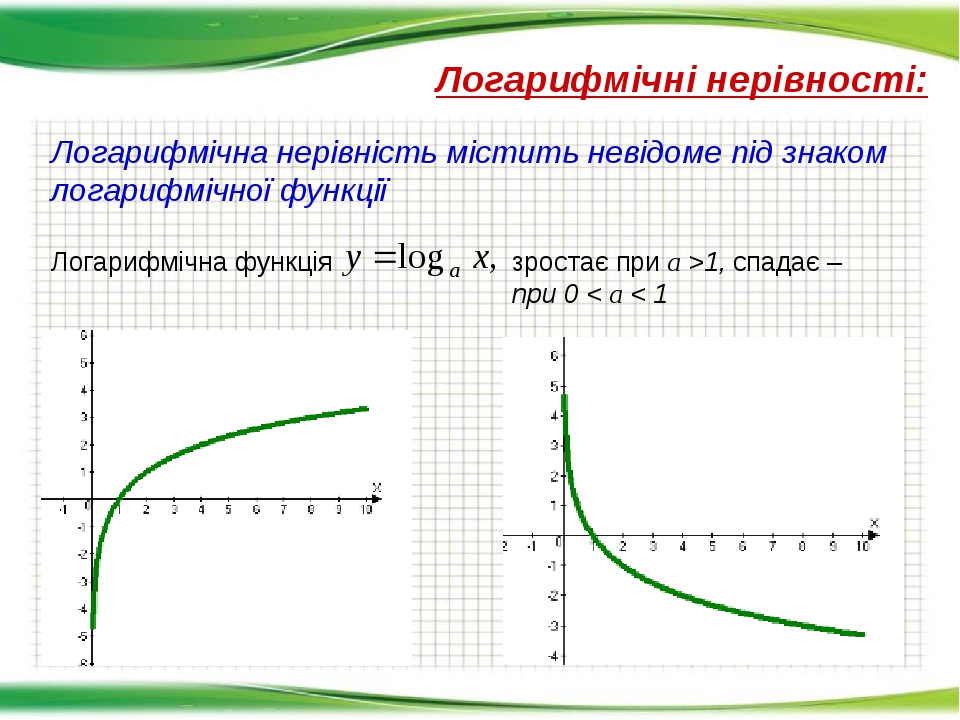
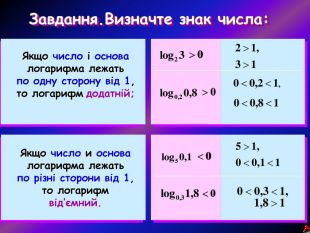
Розв'язання логарифмічних нерівностей ґрунтується на монотонності логарифмічної функції. Тому розв'язання нерівностей вигляду logaf(x)>logag(x) зводиться до розв'язання відповідних нерівностей для функцій f(x) і g(x). Якщо основа a>1, то переходять до нерівності f(x)>g(x) (знак нерівності не змінюється), оскільки в цьому випадку логарифмічна функція зростаюча. Якщо основа 0<a<1, то переходять до нерівності f(x)<g(x) (знак нерівності змінюється), оскільки в цьому випадку логарифмічна функція спадна.В обох випадках додатково знаходять ОДЗ :
{f(x)>0g(x)>0 (за умови, що основа a>0,a≠1 ) Отримана множина розв'язків нерівності повинна входити в ОДЗ, тому знаходять перетин множин.Приклад:Розв'яжи нерівність: log2(3−x)<−1
Розв'язання log2(3−x)<−1ОДЗ:log2(3−x)<log22−13−x>0log2(3−x)<log20,5−x>−33−x<0,5x<3−x<0,5−3x∈(−∞;3)−x<−2,5x>2,5x∈(2,5;+∞) {x∈(2,5;+∞)x∈(−∞;3)
Відповідь: x∈(2,5;3)
Розв'язання
log0,5(x−2)≥log0,5(2x−12)
Розв'язання
ОДЗ:{x−2>02x−12>0{x>22x>12{x>2x>6⇒x>6x∈(6;+∞) log0,5(x−2)≥log0,5(2x−12)x−2x≤x−12x−2x≤−12+2−x≤−10x≥10 {x∈[10;+∞)x∈(6;+∞)
Відповідь: x∈[10;+∞)
Подивіться відео.
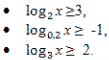
log2(x-3)>5.
log3(x-4)≤log38.
log0,1x>log0,1.(2х + 3).
logπx>logπ3+logπ5.
18.11.2020. УРОК 34


16.11.2020. УРОКИ 32 і 33

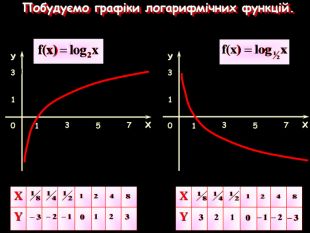
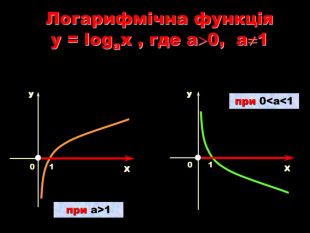
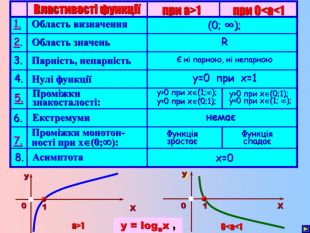
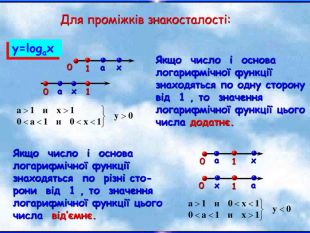
Знак нерівності зберігається.
Приклад 1
Розвяжіть нерівність: 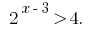
Розвязання:
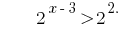
Функція 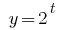 є зростаючою, отже прирівнюємо показники,
є зростаючою, отже прирівнюємо показники,
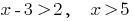
Відповідь: 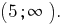
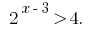
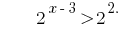
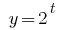 є зростаючою, отже прирівнюємо показники,
є зростаючою, отже прирівнюємо показники,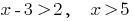
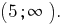
 При 0 < а < 1
При 0 < а < 1
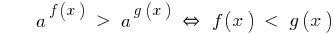
Знак нерівності змінюється на протилежний.
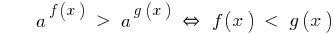
Приклад 2
Розвяжіть нерівність: 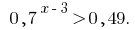
Розвязання:
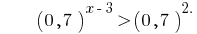
Функція y=0,7^t~ є спадною, отже прирівнюємо показники,
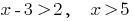
Відповідь: 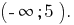
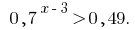
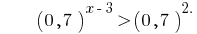
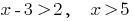
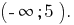
Розвязування більш складніших показникових нерівностей
Приклад 3
Розвяжіть нерівність: 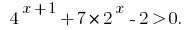
Розвязання:
Заміна 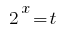 дає нерівність
дає нерівність 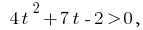
розвязки якої 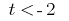 або
або 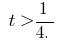
Отже 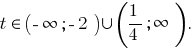
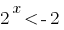 (розвязків немає) або
(розвязків немає) або 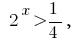 звідки
звідки 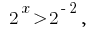 тобто
тобто 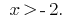
Відповідь: 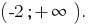
За допомогою загального методу інтервалів
Застосовуємо загальний метод інтервалів,
- Знайти ОДЗ
- Знайти нулі функції

- Позначити нулі функції на ОДЗ і знайти знак
 у кожному з проміжків, на які розбивається ОДЗ.
у кожному з проміжків, на які розбивається ОДЗ. - Записати відповідь, ураховуючи знак нерівності.
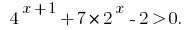

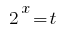 дає нерівність
дає нерівність 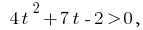
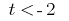 або
або 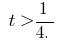
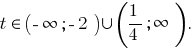
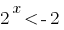 (розвязків немає) або
(розвязків немає) або 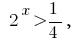 звідки
звідки 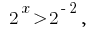 тобто
тобто 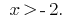
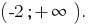

 у кожному з проміжків, на які розбивається ОДЗ.
у кожному з проміжків, на які розбивається ОДЗ.Приклад 4
Розвяжіть нерівність: 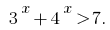
Розвязання:
Розвяжемо нерівність методом інтервалів. Задана нерівність івносильна нерівності 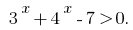
Позначимо 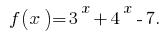
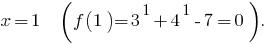
- ОДЗ:
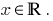
- Нулі функції:
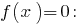
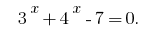
- Оскільки функція
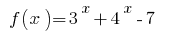 є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення:
є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення: - Позначимо нуль функції на ОДЗ, знаходимо знак
 у кожному з проміжків, на які розбвається ОДЗ, і записуємо розвязки нерівності
у кожному з проміжків, на які розбвається ОДЗ, і записуємо розвязки нерівності 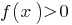
Відповідь: 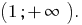
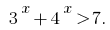

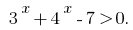
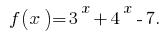
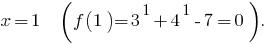
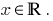
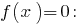
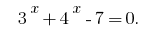
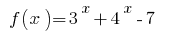 є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення:
є зростаючою, то значення, що дорівнює нулю, вона набуває тільки в одній точці області визначення: у кожному з проміжків, на які розбвається ОДЗ, і записуємо розвязки нерівності
у кожному з проміжків, на які розбвається ОДЗ, і записуємо розвязки нерівності 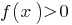
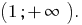
4.11.2020. УРОК 28
Відео
2.11.2020.
УРОКИ 26 і 27
Вивчення математики подібне до Нілу,
що починається невеликим струмком,
а закінчується – великою річкою.
Ч. К. Колтон

28.10.2020.
Відео
Уважно перегляньте відео і в підручнику прочитайте §2 стор.15-16. Виконайте в зошиті завдання №49,51,53 стор.19.
26.10.2020. УРОКИ 23 і 24Тема:Показникова функція та ії властивості.
Перегляньте відео
Відео
Откройте підручник на сторінці 7, прочитайте уважно §1
Математиshkola.in.ua › 1123-matematyka-11-klas-bevz-2019
Відповідаємо на запитання "Перевірте себе". Виконуємо завдання №№1 -7 усно і № 8, 12, 24 пісьмово.
Дорогі учні, запрошую всіх на ОНЛАЙН - УРОК-ПРЕЗЕНТАЦІЮ з теми "Показникова функція в житті людини", який відбудеться о 10:45 .
21.10.2020.
1. Точка А (3; -1; 0), точка В (7; 5; -4). Знайдіть координати середини відрізка АВ.
2. Точка А (3; -1; 0), точка В (7; 5; -4). Знайдіть довжину відрізка АВ.
2. Точка А (3; -1; 0), точка В (7; 5; -4). Знайдіть довжину відрізка АВ.
3. Точка А (3; -1; 0), точка В (7; 5; -4). Знайдіть координати вектора АВ.
3. Точка А (3; -1; 0), точка В (7; 5; -4). Знайдіть координати вектора АВ.
4. Укажіть точку, симетричну точці А(2;-1;6) відносно початку координат.
4. Укажіть точку, симетричну точці А(2;-1;6) відносно початку координат.
5. Укажіть точку, симетричну точці А(5;-2;3) відносно площини XОY.
5. Укажіть точку, симетричну точці А(5;-2;3) відносно площини XОY.
6. Укажіть місце розташування точки А (0; -5; 0)
6. Укажіть місце розташування точки А (0; -5; 0)
7. Знайдіть скалярний добуток вектоів х̅ = (1; 2; - 3) і у̅ = ( -8; 2; 4).
7. Знайдіть скалярний добуток вектоів х̅ = (1; 2; - 3) і у̅ = ( -8; 2; 4).
8. Знайти скалярний добуток векторів, якщо їх модулі дорівнюють 12 та 7 , а кут між ними 45о .
8. Знайти скалярний добуток векторів, якщо їх модулі дорівнюють 12 та 7 , а кут між ними 45о .
9. При якому значенні n вектори ̅а(3;-4;1) і ̅в(n;8;-2) колінеарні?
9. При якому значенні n вектори ̅а(3;-4;1) і ̅в(n;8;-2) колінеарні?
10. При яких значеннях х вектори m̅ (-2; х; 3) і n̅ (5; -2; 4) перпендикулярні?
10. При яких значеннях х вектори m̅ (-2; х; 3) і n̅ (5; -2; 4) перпендикулярні?
11. Точка С - середина АВ.
Знайдіть координати точки А, якщо В (4; -2; -3), С (5; 3; -2).
11. Точка С - середина АВ.
Знайдіть координати точки А, якщо В (4; -2; -3), С (5; 3; -2).
Бажаю успіху!
Математиshkola.in.ua › 1123-matematyka-11-klas-bevz-2019
Відповідаємо на запитання "Перевірте себе". Виконуємо завдання №№1 -7 усно і № 8, 12, 24 пісьмово.
21.10.2020

© http://pozdravok.ru/pozdravleniya/prazdniki/den-znaniy/4.htmДорогі учні! Закладам профтехосвіти рекомендовано перейти на дистанційне навчання на період з 15 жовтня до 15 листопада
Щопонеділка для вас буде проведено два уроки математики. Рекомендується коротко конспектувати уроки, виконувати завдання, тести та контрольну роботу в зошиті. Слідкуйте за подальшими вказівками.
Будьте уважними, бажаю удачі. З усіх питань телефонуйте 095 208 3868 Руднєва Тетяна Михайлівна
19.10.2020. УРОКИ 1 і 2.
ТЕМА: Координати і вектори у просторі.
Запитання 9
Дано: вектор АВ̅( -9; 1; 3), точка А∈Оу, точка В∈(Охz).
Знайти: координати точок А, В.
Запитання 11
Удачи.
Шановні учні групи № 5! Вирішивши контрольну роботу і надавши ії мені будь - яким, зручним для вас, способом ви отримуєте підсумкову оцінку по пройденної темі, оцінки за друге півріччя і за рік.
095 208 3868 Руднєва Тетяна Михайлівна.
27.04.2020. УРОКИ 12 і 13.
ТЕМА: Контрольна робота з теми: "Інтеграл та його застосування".
- Навчальна: перевірити рівень знань учнів, передбачений програмою з цього тематичного блоку, і вміння застосовувати отримані знання під час розв'язування задач;
- Розвиваюча: розвивати вміння виконувати завдання застосовуючи набуті знання;
- Виховна: виховувати наполегливість; вміння робити правильні висновки та бачити кінцеву мету;
- Загальнонавчальні: спроможність організовувати власну діяльність під час виконання завдань

 б)
б)  в)
в)  г)
г)  д)
д) 
2. ( 0,5 бала) Обчислити інтеграл

 А
А 
 Б
Б 
 В
В 
 Г
Г 



 , графік якої проходить через точку А
, графік якої проходить через точку А .
.
УДАЧИ.
22.04.2020. УРОКИ 10 і 11.
ТЕМА: Підготовка до контрольної роботи по темі "Інтеграл та його застосування".
Приклад1.
Приклад 3.
Нещодавно археологи при розкопуванні стародавніх поселень знайшли жертовне місце, яке їх дуже зацікавило. Після досліджень було з’ясовано, що це тіло, утворене обертанням параболи у = – х2 + 2х + 3 навколо вісі Ох (х вчені вимірювали в метрах). Причому виготовлений він був з каменю густиною 2500 кг/м3. Яка масу каменя використали на виготовлення цього жертовника стародавні майстри?
Знайти площу пелюстка ромашки, який розміщено між дугами парабол
Приклад 6.
А зараз перевірь себе.
Тестування.
15.04.2020. УРОКИ 8 і 9. ТЕМА: Тематичні тести.
Перейдіть за посиланням і побачите ваш підручник з математики. На сторінці 71 ви побачите Скарбничку досягнень і набутих компетентностей. Уважно прочитайте, вивчіть та використовуйте при рішенні математичних тестів, яки ви побачите на сторінках 74-75.

Заповніть табліцу, где в верхньому рядку номер завдання, а в ніжньому - варіант відповіді.
Всім успіху.
8.04.2020. середа.
УРОКИ 5 , 6 і 7.
ТЕМА: Застосування визначених інтегралов.
1.04.2020. середа. УРОКИ 3 і 4
“Визначений інтеграл. Формула Ньютона-Лейбніца”.
Мета: сформувати поняття криволінійної трапеції та визначеного інтеграла; домогтися засвоєння формули Ньютона – Лейбніца; сформувати вміння розв’язувати задачі, що передбачають використання поняття інтеграла та формули Ньютона – Лейбніца; показати міжпредметний зв’язок математики та та інших предметів.
1.Смотрите видео -уроки по теме.
.
Результаты поискВидео
2.Запишите конспект в тетради.
Напоминание об основном определении первообразной и неопределенного интеграла










3.Решите самостоятельно.
1.. Вычислить площадь фигуры, ограниченной линиями: ; .
3. Найдите площадь фигуры, ограниченной линиями у = х2 + 2, х = 1, х = -2
4. . Найдите площадь фигуры, ограниченной линиями у = х - 3, у = х2 -3.
УДАЧИ.










































 .
. .
.


